If V X W = <0,-1,0> and V * W = 5, Find Tan(Theta), Where Theta Is the Angle Between V and W.
In this series of posts on "Physical object Spotting for Dummies", we will work through several canonical concepts, algorithms, and touristed deep learning models for fancy processing and protest sensing. Hopefully, it would be a discriminating read for people with no experience in this playing field just want to learn to a greater extent. The Part 1 introduces the concept of Gradient Vectors, the HOG (Histogram of Oriented Gradients) algorithm, and Exclusive Search for pictur segmentation.
I've never worked in the field of computer vision and has no idea how the trick could work when an self-governing auto is configured to tell apart a stop sign from a pedestrian in a red hat. To actuate myself to check over the maths behind object identification and detection algorithms, I'm composition a few posts on this topic "Object Detection for Dummies". This post, part 1, starts with super underlying concepts in image processing and a a few methods for image segmentation. Nothing related to deep neural networks yet. Deep acquisition models for object sensing and acknowledgement volition be discussed in Part 2 and Part 3.
Disclaimer: When I started, I was exploitation "targe identification" and "object detection" interchangeably. I don't think they are the same: the other is more just about apprisal whether an physical object exists in an simulacrum while the latter needs to spot where the object is. However, they are highly related and many object recognition algorithms lay the foundation for detecting.
Golf links to all the posts in the series: [Part 1] [Part 2] [Part 3] [Part 4].
- Image Gradient Transmitter
- Common Image Processing Kernels
- Example: Manu in 2004
- Histogram of Minded Gradients (HOG)
- How HOG works
- Example: Manu in 2004
- Image Partition (Felzenszwalb's Algorithm)
- Graph Construction
- Key Concepts
- How Image Sectionalization Works
- Example: Manu in 2013
- Selective Look for
- How Selective Search Works
- Configuration Variations
- References
Image Slope Vector
First of all, I would like to make sure we stool distinguish the following terms. They are very similar, closely consanguineous, but not exactly the Sami.
| Derived | Directional Differential coefficient | Gradient | |
| Value type | Scalar | Scalar | Vector |
| Definition | The rate of change of a function \(f(x,y,z,...)\) at a breaker point \((x_0,y_0,z_0,...)\), which is the slope of the tan line at the point. | The instant rate of exchange of \(f(x,y,z, ...)\) in the direction of an unit vector \(\vec{u}\). | It points in the direction of the sterling rate of increase of the function, containing wholly the partial derivative information of a multivariable purpose. |
In the image processing, we want to know the direction of colors changing from one extreme to the other (i.e. unfortunate to white happening a grayscale image). Therefore, we want to measure "gradient" happening pixels of colours. The gradient on an image is discrete because from each one pel is independent and cannot be further split.
The image gradient vector is defined as a metric for all individual pixel, containing the pixel color changes in both x-axis and y-axis. The definition is straight with the gradient of a continuous multi-variant function, which is a vector of partial derivatives of all the variables. Suppose f(x, y) records the color of the pixel at location (x, y), the gradient vector of the picture element (x, y) is defined as follows:
\[\begin{align*} \nabla f(x, y) = \begin{bmatrix} g_x \\ g_y \goal{bmatrix} = \begin{bmatrix} \frac{\coloured f}{\partial x} \\[6pt] \frac{\coloured f}{\partial y} \end{bmatrix} = \set out{bmatrix} f(x+1, y) - f(x-1, y)\\ f(x, y+1) - f(x, y-1) \end{bmatrix} \end{adjust*}\]
The \(\frac{\uncomplete f}{\partial x}\) term is the partial on the x-centering, which is computed as the color difference betwixt the adjacent pixels on the left and right of the direct, f(x+1, y) - f(x-1, y). Similarly, the \(\frac{\partial f}{\partial y}\) terminal figure is the partial differential coefficient on the y-focussing, measured as f(x, y+1) - f(x, y-1), the color deviation 'tween the adjacent pixels above and on a lower floor the mark.
There are cardinal important attributes of an image gradient:
- Magnitude is the L2-average of the vector, \(g = \sqrt{ g_x^2 + g_y^2 }\).
- Direction is the arctangent of the ratio betwixt the overtone derivatives on two directions, \(\theta = \arctan{(g_y / g_x)}\).
![]()
Fig. 1. To compute the gradient transmitter of a aim pel at location (x, y), we necessitate to have intercourse the colours of its iv neighbors (or eight surrounding pixels depending on the kernel).
The gradient transmitter of the example in Fig. 1. is:
\[\begin{align*} \nabla f = \begin{bmatrix} f(x+1, y) - f(x-1, y)\\ f(x, y+1) - f(x, y-1) \remnant{bmatrix} = \begin{bmatrix} 55-105\\ 90-40 \end{bmatrix} = \begin{bmatrix} -50\\ 50 \close{bmatrix} \end{align*}\]
Thus,
- the order of magnitude is \(\sqrt{50^2 + (-50)^2} = 70.7107\), and
- the focusing is \(\arctan{(-50/50)} = -45^{\circ}\).
Repeating the slope computing process for every pixel iteratively is too slow. Instead, it can be well translated into applying a convolution operator on the entire prototype matrix, labeled as \(\mathbf{A}\) using one of the specially designed convolutional kernels.
Let's start with the x-direction of the example in Fig 1. using the sum \([-1,0,1]\) slippy ended the x-axis; \(\ast\) is the convolution operator:
\[\lead off{align*} \mathbf{G}_x &= [-1, 0, 1] \ast [105, 255, 55] = -105 + 0 + 55 = -50 \end{align*}\]
Similarly, happening the y-focusing, we adopt the kernel \([+1, 0, -1]^\top\):
\[\begin{align*} \mathbf{G}_y &= [+1, 0, -1]^\top side \ast \get{bmatrix} 90\\ 255\\ 40 \end{bmatrix} = 90 + 0 - 40 = 50 \death{align*}\]
Try this in python:
import numpy every bit Np import scipy.signal as sig data = np . raiment ([[ 0 , 105 , 0 ], [ 40 , 255 , 90 ], [ 0 , 55 , 0 ]]) G_x = sig . convolve2d ( data , np . regalia ([[ - 1 , 0 , 1 ]]), mode = 'valid' ) G_y = sig . convolve2d ( data , np . range ([[ - 1 ], [ 0 ], [ 1 ]]), way = 'valid' ) These 2 functions return array([[0], [-50], [0]]) and array([[0, 50, 0]]) respectively. (Take note that in the numpy array representation, 40 is shown ahead of 90, so -1 is listed in front 1 in the kernel correspondingly.)
Common Image Processing Kernels
Prewitt hustler: Rather than only relying connected four directly adjacent neighbors, the Prewitt operator utilizes viii surrounding pixels for smoother results.
\[\mathbf{G}_x = \begin{bmatrix} -1 & 0 & +1 \\ -1 &ere; 0 &A; +1 \\ -1 & 0 &adenosine monophosphate; +1 \end{bmatrix} \ast \mathbf{A} \text{ and } \mathbf{G}_y = \begin{bmatrix} +1 & +1 & +1 \\ 0 & 0 &adenosine monophosphate; 0 \\ -1 &adenosine monophosphate; -1 & -1 \end{bmatrix} \ast \mathbf{A}\]
Sobel operator: To emphasize the impact of directly adjacent pixels more, they get assigned with high weights.
\[\mathbf{G}_x = \begin{bmatrix} -1 & 0 &A; +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix} \ast \mathbf{A} \text{ and } \mathbf{G}_y = \get down{bmatrix} +1 & +2 & +1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{bmatrix} \ast \mathbf{A}\]
Varied kernels are created for different goals, such atomic number 3 edge detection, blurring, sharpening and many more. Check this wiki page for more examples and references.
Model: Manu in 2004
Countenance's run a simple experiment on the photograph of Manu Ginobili in 2004 [Download See] when he yet had a lot of hair. For simplicity, the photo is reborn to grayscale first. For colored images, we right need to repeat the same cognitive process in each color channel respectively.

Libyan Islamic Fighting Group. 2. Manu Ginobili in 2004 with hair. (Image source: Manu Ginobili's bald-headed spot through the years)
import numpy as nurse clinician meaning scipy import scipy.signal as sig # With mode="L", we force the image to embody parsed in the grayscale, so it is # actually unnecessary to convert the photo color beforehand. img = scipy . misc . imread ( "manu-2004.jpg" , mode = "L" ) # Define the Sobel operator kernels. kernel_x = np . array ([[ - 1 , 0 , 1 ],[ - 2 , 0 , 2 ],[ - 1 , 0 , 1 ]]) kernel_y = np . array ([[ 1 , 2 , 1 ], [ 0 , 0 , 0 ], [ - 1 , - 2 , - 1 ]]) G_x = sig . convolve2d ( img , kernel_x , manner = 'duplicate' ) G_y = sig . convolve2d ( img , kernel_y , style = 'Sami' ) # Plot them! fig = plt . figure () ax1 = fig . add_subplot ( 121 ) ax2 = fig . add_subplot ( 122 ) # Actually plt.imshow() can handle the measure scale well even if I assume't do # the transformation (G_x + 255) / 2. ax1 . imshow (( G_x + 255 ) / 2 , cmap = 'gray' ); ax1 . set_xlabel ( "Gx" ) ax2 . imshow (( G_y + 255 ) / 2 , cmap = 'gray' ); ax2 . set_xlabel ( "Gy" ) plt . show () 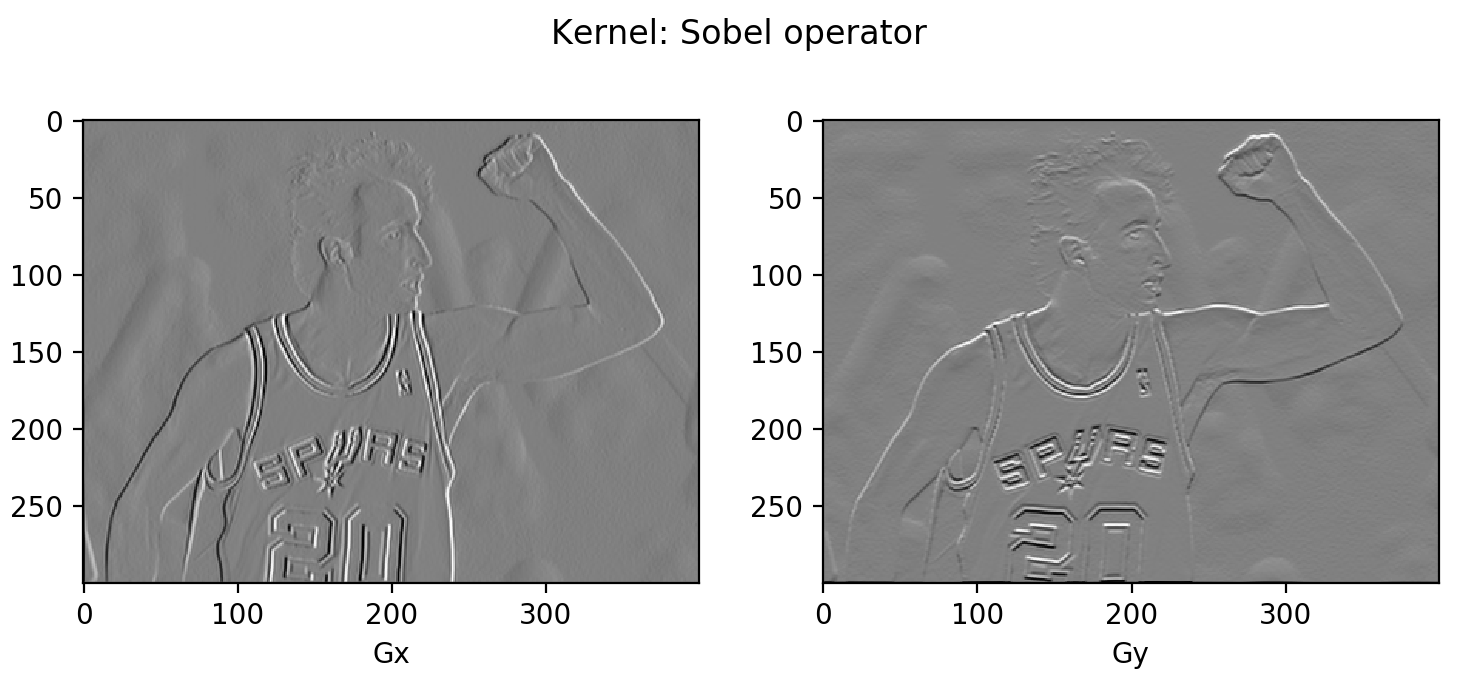
Fig. 3. Go for Sobel operator kernel on the example image.
You might notice that most area is in grayish. Because the difference between two pixel is between -255 and 255 and we penury to convert them stake to [0, 255] for the display purpose. A needled linear transmutation (\(\mathbf{G}\) + 255)/2 would interpret all the zeros (i.e., constant colored downpla shows no change in slope) as 125 (shown as grayness).
Histogram of Oriented Gradients (HOG)
The Histogram of Oriented Gradients (HOG) is an efficient way to extract features out of the pixel colours for building an object recognition classifier. With the knowledge of image gradient vectors, it is non concentrated to understand how HOG works. Lease's start!
How HOG works
1) Preprocess the image, including resizing and colourize normalization.
2) Figure the gradient vector of every pixel, as well as its magnitude and direction.
3) Divide the image into many 8x8 picture element cells. In each cell, the magnitude values of these 64 cells are binned and cumulatively added into 9 buckets of unsigned direction (no polarity, then 0-180 degree kind of than 0-360 stage; this is a practical choice supported empirical experiments).
For better robustness, if the direction of the slope transmitter of a pixel lays between deuce buckets, its magnitude does not all go into the closer one but proportionally cleave between two. For exercise, if a pixel's gradient vector has magnitude 8 and degree 15, it is betwixt 2 buckets for degree 0 and 20 and we would assign 2 to pail 0 and 6 to bucket 20.
This engrossing configuration makes the histogram much more horse barn when small distortion is practical to the project.
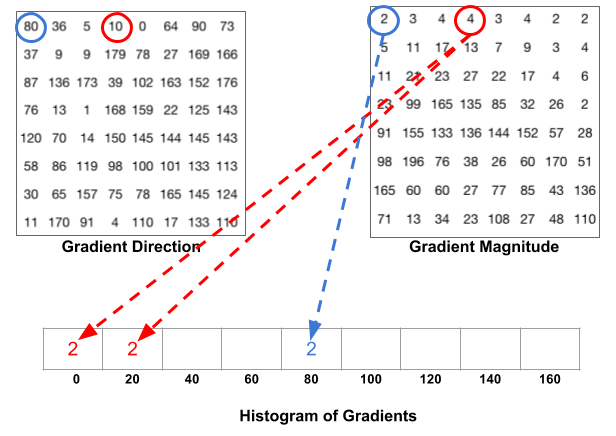
Fig. 4. How to cleave one slope vector's magnitude if its degress is between two degree bins. (Image source: https://www.learnopencv.com/histogram-of-oriented-gradients/)
4) Then we slide a 2x2 cells (thus 16x16 pixels) block crosswise the image. In all deflect region, 4 histograms of 4 cells are concatenated into linear vector of 36 values and then normalized to have an unit weight. The final HOG feature vector is the concatenation of complete the block vectors. IT can be fed into a classifier like SVM for eruditeness object recognition tasks.
Example: Manu in 2004
Rent out's reuse the same good example image in the previous section. Remember that we wealthy person computed \(\mathbf{G}_x\) and \(\mathbf{G}_y\) for the whole image.
N_BUCKETS = 9 CELL_SIZE = 8 # Each cell is 8x8 pixels BLOCK_SIZE = 2 # Each block is 2x2 cells def assign_bucket_vals ( m , d , bucket_vals ): left_bin = int ( d / 20. ) # Manage the case when the direction is between [160, 180) right_bin = ( int ( d / 20. ) + 1 ) % N_BUCKETS verify 0 <= left_bin < right_bin < N_BUCKETS left_val = m * ( right_bin * 20 - d ) / 20 right_val = m * ( d - left_bin * 20 ) / 20 bucket_vals [ left_bin ] += left_val bucket_vals [ right_bin ] += right_val def get_magnitude_hist_cell ( loc_x , loc_y ): # (loc_x, loc_y) defines the top left box of the target cell. cell_x = G_x [ loc_x : loc_x + CELL_SIZE , loc_y : loc_y + CELL_SIZE ] cell_y = G_y [ loc_x : loc_x + CELL_SIZE , loc_y : loc_y + CELL_SIZE ] magnitudes = nurse clinician . sqrt ( cell_x * cell_x + cell_y * cell_y ) directions = neptunium . abs ( np . arc tangent ( cell_y / cell_x ) * 180 / np . pi ) buckets = np . linspace ( 0 , 180 , N_BUCKETS + 1 ) bucket_vals = np . zeros ( N_BUCKETS ) map ( lambda ( m , d ): assign_bucket_vals ( m , d , bucket_vals ), zip ( magnitudes . flatten out (), directions . flatten ()) ) return bucket_vals def get_magnitude_hist_block ( loc_x , loc_y ): # (loc_x, loc_y) defines the top left corner of the object block. return reduce ( lambda arr1 , arr2 : nurse practitioner . concatenate (( arr1 , arr2 )), [ get_magnitude_hist_cell ( x , y ) for x , y in zip ( [ loc_x , loc_x + CELL_SIZE , loc_x , loc_x + CELL_SIZE ], [ loc_y , loc_y , loc_y + CELL_SIZE , loc_y + CELL_SIZE ], )] ) The pursuing code simply calls the functions to construct a histogram and plot information technology.
# Unselected location [200, 200] as an example. loc_x = loc_y = 200 ydata = get_magnitude_hist_block ( loc_x , loc_y ) ydata = ydata / Np . linalg . norm ( ydata ) xdata = range ( len ( ydata )) bucket_names = np . tile ( np . arange ( N_BUCKETS ), BLOCK_SIZE * BLOCK_SIZE ) assert len ( ydata ) == N_BUCKETS * ( BLOCK_SIZE * BLOCK_SIZE ) assert len ( bucket_names ) == len ( ydata ) plt . figure ( figsize = ( 10 , 3 )) plt . bar ( xdata , ydata , align = 'center' , alpha = 0.8 , width = 0.9 ) plt . xticks ( xdata , bucket_names * 20 , rotation = 90 ) plt . xlabel ( 'Direction buckets' ) plt . ylabel ( 'Magnitude' ) plt . grid ( ls = '--' , color = 'k' , alpha = 0.1 ) plt . title ( "HOG of block at [%d, %d]" % ( loc_x , loc_y )) plt . tight_layout () In the inscribe higher up, I use the block with top left corner set at [200, 200] as an lesson and Here is the final normalized histogram of this block. You can wager with the code to change the block emplacemen to be known past a sliding window.
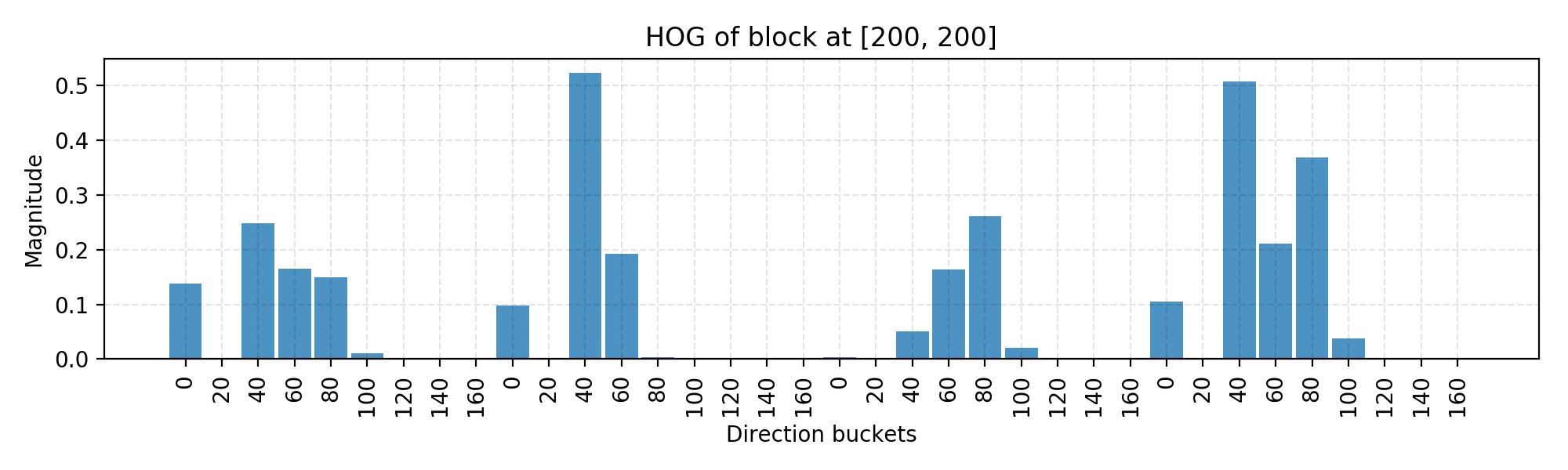
Fig. 5. Demonstration of a HOG histogram for one jam.
The encode is largely for demonstrating the computation process. On that point are many off-the-shelf libraries with HOG algorithm implemented, so much A OpenCV, SimpleCV and scikit-image.
Image Segmentation (Felzenszwalb's Algorithm)
When in that respect exist quintuple objects in one image (true for almost every real-world photos), we ask to identify a part that possibly contains a target object so that the classification can be executed more than efficiently.
Felzenszwalb and Huttenlocher (2004) projected an algorithmic program for segmenting an image into similar regions victimisation a graphical record-based approach. Information technology is also the low-level formatting method for Selective Search (a popular region proposal algorithm) that we are gonna discuss later.
Say, we use a planless graph \(G=(V, E)\) to stand for an input signal image. One vertex \(v_i \in V\) represents unmatched picture element. One edge \(e = (v_i, v_j) \in E\) connects two vertices \(v_i\) and \(v_j\). Its associated burthen \(w(v_i, v_j)\) measures the dissimilarity between \(v_i\) and \(v_j\). The unsimilarity can be quantified in dimensions like colour, location, intensity, etc. The higher the weight, the less similar two pixels are. A segmentation solution \(S\) is a partition of \(V\) into multiple connected components, \(\{C\}\). Intuitively similar pixels should belong to the same components while dissimilar ones are assigned to unlike components.
Graph Construction
At that place are two approaches to constructing a graph come out of the closet of an image.
- Grid Graph: Each pixel is only if connected with circumferent neighbours (8 other cells in add up). The edge weight is the absolute difference between the loudness values of the pixels.
- Closest Neighbor Graph: Each pixel is a period in the feature space (x, y, r, g, b), in which (x, y) is the pixel location and (r, g, b) is the tinge values in RGB. The weight is the Euclidean distance between two pixels' feature vectors.
Key Concepts
Before we make the criteria for a good graph partition (aka mental image segmentation), let us define a couple of winder concepts:
- Internecine difference: \(Int(C) = \max_{e\in MST(C, E)} w(e)\), where \(MST\) is the minimal spanning tree of the components. A component part \(C\) can still remain connected even when we have removed entirely the edges with weights < \(Int(C)\).
- Divergence between two components: \(Dif(C_1, C_2) = \min_{v_i \in C_1, v_j \in C_2, (v_i, v_j) \in E} w(v_i, v_j)\). \(Dif(C_1, C_2) = \infty\) if there is nary edge in-betwixt.
- Minimum internal difference: \(MInt(C_1, C_2) = min(Int(C_1) + \tau(C_1), Int(C_2) + \tau(C_2))\), where \(\tau(C) = k / \vert C \vert\) helps make sure we rich person a pregnant threshold for the remainder between components. With a high \(k\), it is more belik to result in larger components.
The quality of a segmentation is assessed by a pairwise region comparison predicate defined for inclined two regions \(C_1\) and \(C_2\):
\[D(C_1, C_2) = \begin{cases} \text{True} &ere; \text{ if } Dif(C_1, C_2) > MInt(C_1, C_2) \\ \text{False} &ere; \text{ otherwise} \end{cases}\]
Only the predicate holds True, we consider them as two independent components; otherwise the segmentation is too fine and they likely should be merged.
How Image Segmentation Full treatmen
The algorithm follows a bottom-up procedure. Given \(G=(V, E)\) and \(|V|=n, |E|=m\):
- Edges are sorted aside weight in ascending order, labeled as \(e_1, e_2, \dots, e_m\).
- Initially, each pixel stays in its have component, so we start with \(n\) components.
- Repeat for \(k=1, \dots, m\):
- The segmentation snapshot at the step \(k\) is denoted as \(S^k\).
- We occupy the k-th march in the order, \(e_k = (v_i, v_j)\).
- If \(v_i\) and \(v_j\) belong to the same factor, do nothing and so \(S^k = S^{k-1}\).
- If \(v_i\) and \(v_j\) belong to deuce incompatible components \(C_i^{k-1}\) and \(C_j^{k-1}\) as in the partitioning \(S^{k-1}\), we want to merge them into one if \(w(v_i, v_j) \leq MInt(C_i^{k-1}, C_j^{k-1})\); otherwise do naught.
If you are interested in the proof of the cleavage properties and why it e'er exists, please concern to the report.

Fig. 6. An indoor scene with segmentation detected by the power grid graph construction in Felzenszwalb's chart-settled segmentation algorithm (k=300).
Example: Manu in 2013
This clip I would use of goods and services the photo of past Manu Ginobili in 2013 [Image] as the example image when his bald spot has grown up strong. Notwithstandin for simplicity, we use the picture in grayscale.

Fig. 7. Manu Ginobili in 2013 with bald spot. (Image reservoir: Manu Ginobili's bald-headed spot through the age)
Rather than coding from chafe, get us implement skimage.partitioning.felzenszwalb to the image.
import skimage.segmentation from matplotlib import pyplot as plt img2 = scipy . misc . imread ( "manu-2013.jpg" , mode = "L" ) segment_mask1 = skimage . segmentation . felzenszwalb ( img2 , scale = 100 ) segment_mask2 = skimage . segmentation . felzenszwalb ( img2 , scale = 1000 ) Ficus carica = plt . count on ( figsize = ( 12 , 5 )) ax1 = FIG . add_subplot ( 121 ) ax2 = fig . add_subplot ( 122 ) ax1 . imshow ( segment_mask1 ); ax1 . set_xlabel ( "k=100" ) ax2 . imshow ( segment_mask2 ); ax2 . set_xlabel ( "k=1000" ) fig . suptitle ( "Felsenszwalb's efficient graphical record based image division" ) plt . tight_layout () plt . show () The code ran deuce versions of Felzenszwalb's algorithms as shown in Fig. 8. The left k=100 generates a finer-grained segmentation with small regions where Manu's barefaced topographic point is identified. The right one k=1000 outputs a coarser-grained partitioning where regions tend to be large.

Fig. 8. Felsenszwalb's efficient graph-based image partition is practical on the photo of Manu in 2013.
Discriminating Search
Discriminating search is a common algorithmic program to provide region proposals that potentially contain objects. Information technology is built on top of the image segmentation output and use neighborhood-based characteristics (NOTE: non just attributes of a single pixel) to make a fundament-up graded group.
How Discriminating Search Works
- At the initialisation stage, utilise Felzenszwalb and Huttenlocher's graph-based image segmentation algorithmic program to make regions to start with.
- Use a greedy algorithmic rule to iteratively group regions put together:
- Primary the similarities betwixt all neighbouring regions are calculated.
- The two nearly similar regions are sorted put together, and new similarities are calculated between the resulting region and its neighbours.
- The process of grouping the most similar regions (Step 2) is repeated until the whole image becomes a single region.

Fig. 9. The detailed algorithmic program of Selective Explore.
Configuration Variations
Donated two regions \((r_i, r_j)\), selective look proposed four antonymous similarity measures:
- Color law of similarity
- Texture: Use algorithmic rule that works well for material acknowledgement such as Sieve.
- Size: Small regions are encouraged to merge early.
- Shape: Ideally one region can fill the gap of the other.
Away (i) tuning the threshold \(k\) in Felzenszwalb and Huttenlocher's algorithm, (ii) changing the color space and (iii) pick different combinations of similarity metrics, we can produce a diverse solidification of Selective Search strategies. The version that produces the part proposals with top-grade timber is designed with (i) a mixture of several initial segmentation proposals, (ii) a blend of multiple color spaces and (iii) a combination of all similarity measures. Unsurprisingly we necessitate to balance between the calibre (the model complexness) and the speed.
Cited Eastern Samoa:
@article{weng2017detection1, title = "Objective Detection for Dummies Part 1: Gradient Vector, Hogg, and SS", author = "Weng, Lilian", journal = "lilianweng.github.Io/lil-logarithm", yr = "2017", universal resource locator = "HTTP://lilianweng.github.Io/lil-log/2017/10/29/object-recognition-for-dummies-voice-1.html" } References
[1] Dalal, Navneet, and Circular Triggs. "Histograms of oriented gradients for human detection." Computer Vision and Pattern Recognition (CVPR), 2005.
[2] Pedro F. Felzenszwalb, and Daniel P. Huttenlocher. "Efficient graph-based image partitioning." Intl. journal of computer vision 59.2 (2004): 167-181.
[3] Histogram of Homeward-bound Gradients by Satya Mallick
[4] Slope Vectors aside Chris McCormick
[5] HOG Somebody Detector Tutorial by Chris McCormick
If V X W = <0,-1,0> and V * W = 5, Find Tan(Theta), Where Theta Is the Angle Between V and W.
Source: https://lilianweng.github.io/lil-log/2017/10/29/object-recognition-for-dummies-part-1.html
0 Response to "If V X W = <0,-1,0> and V * W = 5, Find Tan(Theta), Where Theta Is the Angle Between V and W."
Post a Comment